Ces simulations que je vous propose d'utiliser sont construites d'après des règles de calculs mathématiques de variations de fréquences lors de la reproduction sexuée et de la transmission d'une génération à l'autre
(suivant par exemple la loi de Mendel de dissociation des 2 allèles lors de la formation des gamètes chez un individu diploïde).
C'est donc un modèle mathématique qui est à considérer comme tout modèle en sciences:
il montre des faits exacts dans la limite des critères qui ont été utilisés pour le construire.
Il est donc le cas général qui pourra être modifié dans un sens ou un autre si l'allèle est soumis à des intéractions avec d'autres facteurs non pris en compte dans ce cas.
Sélection naturelle
Source: Kent Holsinger - université du Connecticut
p est la fréquence initiale de l'allèle. Ses variations sont lues sur l'axe vertical.
Trois fréquences sont proposées (0.1, 0.5 et 0.9).
w11 est le génotype homozygote récessif.
w12 est le génotype hétérozygote.
W22 est le génotype homozygote dominant.
On attribue à chaque génotype une valeur sélective. Cette valeur sélective découle de la valeur de l'allèle.
Pour rappel de l'article :
- Si elle est neutre (n'accordant aucun avantage ou désavantage de viabilité à l'individu), alors les 3 génotypes bénéficient de la même valeur sélective. Ils confèrent la même viabilité ou capacité de survie et de reproduction aux individus diploïdes porteurs.
w11 = ww12 = ww22
ww1.1 < ww1.2 = ww2.2
ww11 = ww12 < ww22
Toute expérience nécessite de ne faire varier qu'un seul facteur (paramètre) expérimental à la fois afin de pouvoir être interprétée. Dans les situations proposées, on fixera donc à chaque génotype une valeur sélective fixe (ce sont les constantes de l'expérience). On ne fait varier que la fréquence de départ p de l'allèle dans la population qui traduit à quel taux cet allèle est présent dans la population initiale, soit du plus petit 0.1 au plus grand 0.9 et ceci successivement (les 3 courbes s'inscrivent sur le même repère).
Cliquer sur Start pour construire une courbe. Huit peuvent être construites sur le même repère. Cliquer sur Clear pour tout effacer.
Et si vous ne vous sentez pas l'esprit assez ludique (ou concentré)
pour mettre en jeu vous-même les simulations,
des images de copies d'écran vous donnent les résultats visuels des situations proposées.
Les correspondances couleur de courbe-situation testée sont les suivantes :
- gris : p = 0.1
- bleu : p = 0.5
- turquoise : p = 0.9
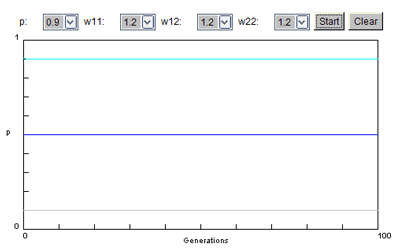
Situation 1 : l'allèle est neutre
Fixer les ww à la même valeur. Vous constatez que la fréquence de l'allèle est maintenue constante dans la population au fil des générations. Si vous changez la valeur ww (en donnant toujours la même à chaque génotype), le constat reste identique: il y a conservation de l'allèle dans la population.
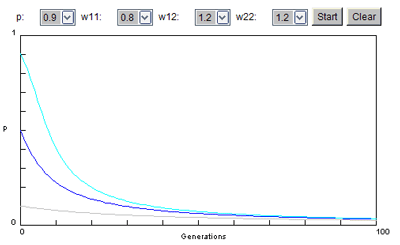
Situation 2 : l'allèle est récessif et négatif dans le milieu où vit la population
On fixe les valeurs adaptatives des différents génotypes ainsi:
ww1.1 = 0.8 ww1.2 = 1.2 ww2.2 = 1.2
Quelle que soit la fréquence de départ de l'allèle, on constate qu'elle tend vers 0 sans s'annuler. Seul varie le nombre de générations conduisant à la fréquence minimale.
Le milieu tend donc bien à éliminer les allèles pathogènes, lesquels restent cependant présents dans la population s'ils sont récessifs.
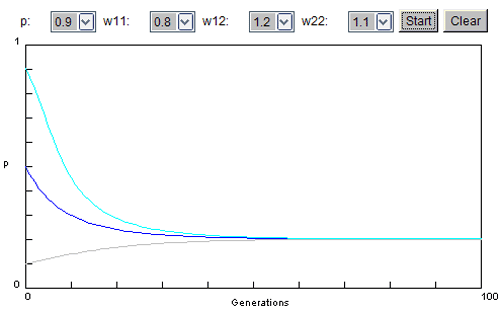
Situation 2 bis : Même situation mais...
Cette fois, le milieu est tel que les hétérozygotes ont une meilleure viabilité que les homozygotes dominants, car si l'allèle recessif est morbide pour le génotype double récessif, il confère une protection contre une autre maladie due au milieu.
Cette situation est notamment celle de l'allèle drépanocytaire, causatif de la drépanocytose, anémie grave diminuant la survie des doubles récessif (quel que soit d'ailleurs le milieu), mais conférant aux hétérozygotes une résistance au paludisme. On considère alors l'évolution de cet allèle dans une région où sévit le paludisme qui est alors un facteur particulier du milieu qui avantage à l'état hétérozygote une allèle morbide. On attribue les valeurs suivantes:
ww1.1 = 0.8 ww1.2 = 1.2 ww2.2 = 1
On constate que la fréquence de cet allèle ne tend plus vers 0. Il est conservé à une fréquence non nulle qui est identique quelle que soit celle de départ.
C'est donc une illustration, par comparaison avec la situation 2, du fait que la valeur d'un allèle se définit toujours dans un milieu donné. Mais aussi dans un temps donné puisqu'une action moderne de démoustication, en faisant disparaître le paludisme, va ramener le milieu et donc l'évolution de l'allèle à la situation 2.
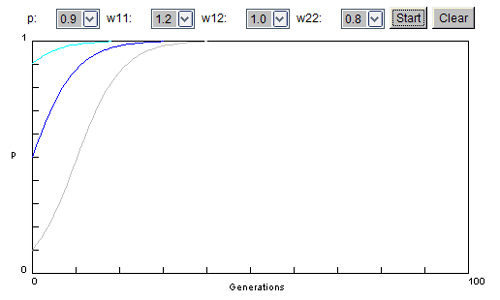
Situation 3 : l'allèle a une valeur positive
Il confère un avantage sélectif. On le considère toujours comme récessif. Les valeurs adaptatives sont :
ww1.1 = 1.2 ww1.2 = 1 ww2.2 = 0.8
Quelle que soit la fréquence de départ, on constate qu'elle augmente jusqu'à ce que cet allèle soit finalement le seul conservé dans la population (p = 1 ou tend vers 1 signifiant que 100% des individus ont cet allèle).
Le milieu tend donc à garder un allèle positif et à augmenter sa fréquence jusqu'à un maximum.
Dans le cadre de l'élevage, il faut considérer que la sélection du milieu n'est plus seule en jeu (et que la taille des sous-populations est bien plus faible que celle sur laquelle ces simulations sont calculées).
Sont donc introduits de nouveaux facteurs qui vont modifier, par exemple, l'évolution constatée dans la deuxième situation. Pour les allèles récessifs délétères, quel que soit le gène considéré, la consanguinité forcée ou la répétition des mariages avec un ou des sujets porteurs vont conserver la fréquence de l'allèle, voire l'augmenter.
C'est vraisemblablement ce qui a été amorcé chez les Abyssins avec l'amyloïdose rénale.
Dans le cas d'un allèle dominant, la valeur adaptative des homozygotes et des hétérozygotes est réduite. On se situe alors plutôt, en élevage, dans la situation suivante:
ww1.1 = 1.2 (meilleure valeur des chats non porteurs de la mutation pathogène) ww1.2 et ww2.2 = 1 (baisse de la valeur adaptative des sujets, qu'ils aient 1 seul ou 2 allèles mutés pathogènes)
Je vous laisse le soin de constater comment évolue la fréquence d'un tel allèle dans une population si aucune intervention ne vient modifier le cours naturel des choses.
Si vous voulez accorder une meilleur valeur adaptative aux hétérozygotes, attribuez 1 à ww1.2 et 0.8 à ww2.2 (mais vous pouvez aussi choisir d'autres valeurs tout en gardant ww1.2 plus grand que ww2.2).
Qu'en pensez-vous ?
Or ce sont les situations de base d'une mutation dominante comme l'est la CMH1, les derniers exemples proposés intégrant la possibilité d'autres facteurs du milieu qui limiteraient la morbidité de l'allèle chez l'hétérozygote (par rapport à l'homozygote). Par contre, il n'est pas possible de modéliser l'action d'autres gènes sur cet allèle avec ce modèle. Tous les facteurs d'une expressivité variable ne peuvent donc être "testés".
Et je vous laisse aussi le soin de réfléchir aux pratiques à cesser et à celles à mettre en œuvre afin d'inverser un tel processus naturel.
Dérive génétique
Source: Kent Holsinger - université du Connecticut
p est la fréquence initiale de l'allèle. Ses variations sont lues sur l'axe vertical.
Trois fréquences sont proposées (0.1, 0.5 et 0.9).
N est le nombre d'individus de la population (10, 25, jusqu'à 1000).
Et les générations vont de 50 à 2500.
On fixe 2 des paramètres afin de pouvoir juger de l'effet de la variable.
Dans la situation testée :
p = 0.5 (valeur par défaut) ;
Le nombre de générations est fixé à 100 ;
La variable est le nombre d'individus de la population.
Les correspondances couleur de courbe-N sont :
- bleu = 10
- turquoise = 25
- rouge = 50
- rose = 100
- jaune = 250
- vert = 1000
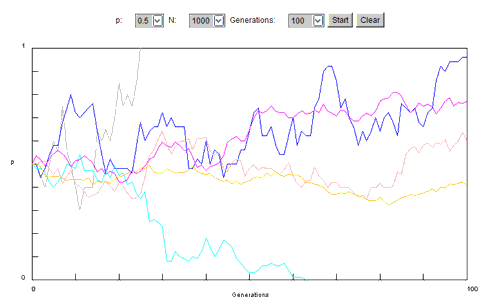
On constate un maintien de l'allèle pour les populations entre 100 et 1000 individus. En dessous de 100, 2 évolutions totalement diffrentes de la fréquence de l'allèle illustrent déjà la notion de dérive, évolution incontrôlée: si l'allèle disparaît pour les petites populations initiales de 10 et 25, par contre, on constate une forte augmentation dans le cas d'une population initiale de 50 individus. Et celle-ci n'est donc plus vérifiée pour les populations de taille supérieure.
On constate la même "anarchie" si on change de variable.
La "dérive génétique" traduit donc ce fait d'une évolution totalement aléatoire de la fréquence d'un allèle suivant des paramètres qui peuvent être sa fréquence initiale, la taille de la population mais aussi le nombre de générations considérées.
Sélection naturelle et dérive génétique
Vous pouvez à présent simuler les effets combinés de la sélection naturelle et de la dérive génétique.
Source: Kent Holsinger - université du Connecticut